2006년 11월 6일 (월) 16:46   한겨레

 

‘엉터리 문제 가려내기’가 수학 첫걸음

[한겨레] 수학개념 쏙쏙 /

■ 교실에 있는 대형 텔레비전에 수학 문제가 나타나자 아이들이 큰 소리로 읽었다.

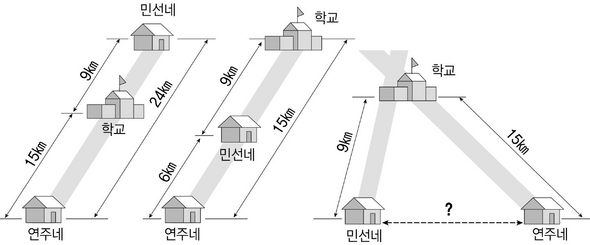
연주와 민선이는 같은 학교에 다닌다. 연주는 학교로부터 15km 떨어진 곳에, 민선이는 9km 떨어진 곳에 산다. 연주와 민선이네 집 사이의 거리는 얼마인가?

문제를 읽자마자 성진이가 큰 소리로 대답했다. “15 더하기 9는 24. 답은 24km입니다.”

그러자 성진이 짝꿍인 주철이가, “아닙니다. 15 빼기 9를 해서 답은 6km입니다.”라고 말했다.

고개를 갸우뚱하던 둘은 누구 답이 맞나 머리를 맞대고 풀기 시작했다. 그러는 사이 맨 앞에 앉은 소정이가 조용히 말했다. “답은 두 가지입니다. 두 사람이 학교와 서로 반대 방향에 산다면 거리는 24km이고, 학교로부터 같은 방향에 산다면 6km입니다.”

여기 저기서, “앗, 그러고 보니 답이 두 개구나.”라는 소리와, “선생님, 정답이 뭐예요?”하는 소리가 들렸다. 선생님이 빙긋이 웃으며, “자, 이제 답을 알겠어요?”라고 말씀하자, 성진이와 주철이가 잔뜩 골이 난 목소리로 퉁명스럽게 말했다. “순 엉터리 문제예요! 두 사람 집이 어디 있는 지도 모르는데 어떻게 풀어요?” “맞아요. 학교와 두 집이 삼각형 모양으로 있을 수도 있잖아요.”




만약 두 집의 위치가 학교와 일직선으로 있다면 소정이의 풀이가 맞지만 일직선이 아닐 경우에는 두 집 사이의 거리를 정확히 알 수 없다. 단, 두 집 사이의 거리가 6km에서 24km 사이라는 것은 알 수 있다.

성진이네 반 아이들은 문제를 읽을 때 깊게 생각하지 않고 읽었다. 수학 문제를 많이 풀다보면 문제 푸는 능력이 좋아지긴 하지만 문제를 정확히 읽지 않는 버릇이 생기기도 한다. 많이 풀다보면 문제들이 다 비슷비슷하다. 그래서 “이런 문제는 원래 이렇게 푸는 거야”하며 습관적으로 문제를 풀기 십상이다. 그러다 자기 답이 틀린 걸 알고 난 뒤, 문제를 찬찬히 읽어 보며 다시 푼다. 하지만, 이번에도 제대로 안 읽어서 또 틀리기도 한다. 그런 실수를 하지 않으려면 문제를 읽을 때 집중해서 읽는 습관을 갖는 것이 좋다. 그렇게 읽다보면, 그 문제가 물어보는 게 무엇인지, 그 문제에 제시된 조건은 무엇인지 알 수 있게 된다.

위 문제에는 학교와 두 아이의 집의 위치 관계를 알 수 있는 조건이 빠져 있다. 따라서 여러 가지 의견이 나올 수밖에 없다. 하지만 문제에 그림이 들어있거나, ‘같은 방향으로 일직선 위에’라는 말이 들어 있었다면 쉽게 풀 수 있었을 것이다.

■ 이번엔 다음 문제를 보자.

유진이는 100m를 18초 만에 달렸다. 그렇다면 1km를 달리는 데는 얼마나 걸릴까?

이 문제에 대한 반응으로 다음 세 가지가 있을 수 있다.

- 18×10=180초, 3분

- 원래는 180초가 나와야 하는데 지치고 힘들기 때문에 200초가 걸린다.

- 그 속도를 계속 유지할 수 없고 계속 느려지기 때문에 시간이 얼마나 걸릴지 알 수 없다.

이 가운데 세번째 의견이 실제적인 상황에 대한 지식을 효과적으로 사용한 답이라고 볼 수 있다. 사실, 이 문제의 답을 정확히 구하려면 ‘같은 속도로 달린다’는 조건이 있었야 했다. 문제에 그런 조건이 없음에도 불구하고, 아무 생각 없이 단순히 18×10이라고 생각했던 사람, 손들어 보자. 문제에 나와 있지도 않은 조건을 만들어서 사용하는 것은 바람직한 수학적인 태도라고 볼 수 없으므로, 조건을 꼼꼼히 살피는 태도를 기르자.

■ 비슷한 문제를 좀 더 알아보자.

연재의 가장 친한 친구는 5명이고 규선이의 친구는 6명입니다. 연재와 규선이의 생일은 같은 날입니다. 그래서 둘은 함께 생일 파티를 하기로 하고 자기 친구들을 모두 초대하였습니다. 연재와 규선이의 생일 파티에 온 친구들을 모두 몇 명입니까?

이 문제는, 언뜻 생각하면 5+6만 계산하면 될 것 같다. 하지만 이 문제를 읽고 다음과 같이 반응을 하는 학생들도 있다.

- 초대를 받았지만 못 올 수도 있으므로 몇 명인지 알 수 없다.

- 연재와 규선이에게 동시에 초대받은 친구가 있을 수 있어서 파티에 온 사람이 몇 명인지 알 수 없다.

- 생일 파티에 온 ‘친구’를 셀 때 연재와 규선이도 세야 하는 지 세지 말아야 하는 지 알 수 없어서 답을 모르겠다.

이런 답을 낸 학생들은, ‘초대를 받았다고 언제나 파티에 참석하는 건 아닌데?’, ‘친구의 의미가 뭐지?’ 라며 깊게 생각하면서 수학 문제 속 상황을 실생활과 똑같이 생각한 것이다.

다음 문제도 풀어보자.

12m 떨어진 두 막대 사이를 연결시켜야 하는데, 가지고 있는 끈은 2m 짜리들 뿐이다. 두 막대를 연결할 수 있으려면 필요한 끈의 수는 몇 개인가?

이 문제에 끈끼리 연결할 때도 끈을 사용해야 하는지, 끈을 연결할 때는 끈을 얼마나 사용하는지가 나와 있지 않다. 따라서 ‘알 수 없다’는 답이 가장 적절하다. ‘끈을 이을 때 사용하는 끈의 길이는 생각하지 않는다.’라는 설명이 들어 있다면, 이 문제를 풀 수 있는 조건이 정확히 설명되어 있으므로 간단히 12÷2를 하면 된다. 하지만 그런 조건이 정확히 나와 있지 않아서 그 문제를 풀 수 없을 경우엔, 필요한 조건이 무엇인지 생각해 보고 문제를 정확히 다듬어 보자. 그러면 문제를 정확히 읽는 습관이 몸에 밸 것이다.

아주 평범하게 보이는 문제라도 그 문제 안에 그 문제를 풀 수 있는 정확한 조건이 들어있는지 없는지를 먼저 생각하면서 풀어야 사고력이 커진다. 그냥 아무 생각 없이 풀면 아무리 많은 수학 문제를 풀어도 사고력은 키워지지 않는다.

강미선/수학 칼럼니스트 upmmt@hanmail.net

* 이 글에 실린 문제들은 <현실적인 문장제에 관한 초등학생의 반응 분석>(이화여대 초등교육과 김민경 교수 2004년 논문)을 참조하였다.